快速幂

为了高效地计算一个数的幂，在计算a^b^时候，可以将时间复杂度由O(b)降低至O(logb)

快速幂算法的原理

快速幂算法的核心思想是利用指数的二进制展开和乘法的结合律。当我们计算 a^b^ 时，我们可以将指数 b分解为多个2的幂的和，例如：

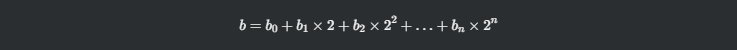
其中 bi 要么是0，要么是1（因为这是二进制表示）。因此，我们可以将 a^b^ 分解为：

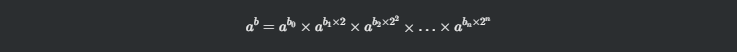
public static long fastPower(long a, long b, long modulus) {
	long res = 1;
	//1.将指数b转换为二进制表示
    while (b > 0) {
    	//2.从b的最低位开始，对于每一位：
    	//如果这一位是1，那么将当前的底数a乘到结果中
    	if ((b & 1) == 1) res = (res * a) % modulus;
        //将底数a自乘（a = a * a)
    	a = (a * a) % modulus;
        //继续处理下一位，直到处理完所有位
    	b = b >> 1;
    }
    return res;
}